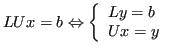Metodo di eliminazione di Gauss
Sia 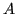 matrice quadrata non singolare.
Nella soluzione con MEG di un sistema
matrice quadrata non singolare.
Nella soluzione con MEG di un sistema 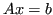 , la matrice
, la matrice 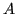 viene trasformata in una matrice triangolare superiore
viene trasformata in una matrice triangolare superiore 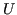 e il sistema viene trasformato nell'equivalente
e il sistema viene trasformato nell'equivalente
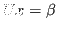 (soluzione identica):
(soluzione identica):
L'algoritmo realizza una decomposizione LU, la quale fattorizza 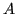 in un prodotto di due matrici
in un prodotto di due matrici 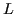 e
e 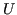 rispettivamente triangolare inferiore e superiore.
rispettivamente triangolare inferiore e superiore.
Quindi il sistema 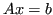 diventa
diventa
Il sistema triangolare 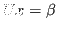 è facilmente risolvibile con sostituzioni all'indietro, di complessità
è facilmente risolvibile con sostituzioni all'indietro, di complessità
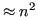 .
.
Questo approccio è estremamente utile quando si ha necessità di trovare la soluzione per diversi sistemi con matrice 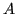 fissa in cui varia solo il termine noto
fissa in cui varia solo il termine noto
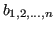 : è sufficiente calcolare
: è sufficiente calcolare 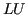 una volta sola a costo
una volta sola a costo 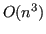 e poi risolvere ciascun sistema a costo
e poi risolvere ciascun sistema a costo 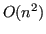 .
.
Subsections
Matteo Lisotto, Tobia Tesan - CC-BY 2.0
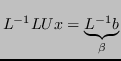
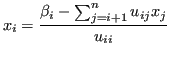
![]() fissa in cui varia solo il termine noto
fissa in cui varia solo il termine noto
![]() : è sufficiente calcolare
: è sufficiente calcolare ![]() una volta sola a costo
una volta sola a costo ![]() e poi risolvere ciascun sistema a costo
e poi risolvere ciascun sistema a costo ![]() .
.