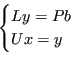Next: Applicazioni del MEG Up: Metodo di eliminazione di Previous: MEG e sistemi malcondizionati Indice Indice analitico
Posto ![]() non singolare:
non singolare:
Trasforma ossia un sistema ![]() , denotato in breve come
, denotato in breve come ![]() , in
, in ![]() .
.
Il sistema
![]() si risolve, ovviamente, con una serie di sostituzioni all'indietro:
si risolve, ovviamente, con una serie di sostituzioni all'indietro:
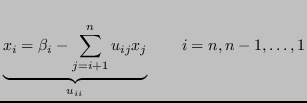
Il costo computazionale è di
![]() FLOPs, e il costo asintotico è:
FLOPs, e il costo asintotico è:
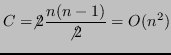
Dunque il costo per risolvere