Next: Cenni sulla soluzione di Up: Metodo di eliminazione di Previous: Applicazioni del MEG Indice Indice analitico
Per risolverli il modo ingenuo può essere, con costo
![]() :
:
Non è però il metodo più intelligente per procedere.
Ricordiamo:
Allora possiamo riscrivere i sistemi come coppie di sistemi triangolari:
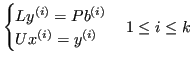
Con ![]() significativi il costo è vantaggioso:
significativi il costo è vantaggioso:

Consideriamo una base ![]() :
:
È notorialmente possibile rappresentare qualunque vettore ![]() dato come:
dato come:
Definiamo ![]() come elemento
come elemento ![]() -esimo della base canonica:
-esimo della base canonica:
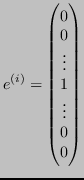
Dunque
![]() .
.
Osserviamo che data una matrice ![]() invertibile vale allora:
invertibile vale allora:
Moltiplicando a sinistra entrambi gli elementi per la matrice ![]() :
:
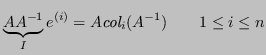
Poichè:
Allora è possibile riformulare il problema come:
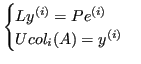
Matteo Lisotto, Tobia Tesan - CC-BY 2.0