Cenni sulla soluzione di sistemi fortemente malcondizionati

Si rammenti per prima cosa:

Definizione 6.20 (Sistema mal condizionato)   Un sistema mal condizionato è un sistema $Ax = b$ t.c.

$$k(A) \gg 1$$

Si consideri:

$$PA=LU \qquad PA\approx \tilde{L}\tilde{U} \qquad \tilde{L}\tilde{U}x = Pb \qquad \Vert PA - \tilde{L}\tilde{U}\Vert \approx eps$$

La fattorizzazione $\tilde{L}\tilde{U}$ è molto buona poichè la distanza da $PA$ è vicina alla precisione di macchina, ma se il sistema è mal condizionato gli effetti possono essere comunque deleteri sulla soluzione.

Si può allora osservare:

$$\frac{\Vert\delta b\Vert}{\Vert b\Vert} \le \varepsilon \to \frac{\Vert\delta x\Vert }{\Vert x\Vert} \approx k(A) \varepsilon$$

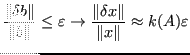
Invece di risolvere $A\tilde{x} = \tilde{b}$, ottenendo una soluzione sbagliata, è possibile risolvere con una famiglia di sistemi tale che:

$$A_h x_h = b \qquad x_h \to x \qquad k(A_h) < k(A)$$

Con:

$$k(A_h) \to_{h \to 0} k(A)$$

Allora:

$$A_h\tilde{x}_h = \tilde{b}$$