Cenno ai sistemi sovradeterminati

Definizione 6.21 (Sistema sovradeterminato)   Un sistema sovradeterminato è un sistema in cui ci sono più equazioni che incognite:

$$Ax = b$$

$$A \in \mathbb{R}^{m\times n}\qquad x\in\mathbb{R}^n\quad b\in R^m\quad n > m$$

In generale il sistema non ha soluzione.

Quello che si può fare è circoscrivere un intorno della soluzione, minimizzando $\Vert Ax-b\Vert _2^2$ con il metodo dei minimi quadrati.

$$\Vert Ax - b\Vert _2^2 = \min \mathit{dist}(Ax,b) = \min \Vert \lbrace \sum_{j=1}^n a_{ij}x_j \rbrace - \lbrace b_i \rbrace$$

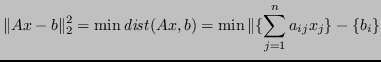
Un caso particolare è:

$$Va = y$$

$V = (v_{ij})$ è matrice di Vandermonde, $\lambda = a$ coefficiente del polinomio dei minimi quadrati, $b = y$ valori campionati.

Allora:

$$Va = y \Leftrightarrow V^tVa=V^ty$$   (equazioni normali)

$$\min{x\in\mathbb{R}^n}\Vert Ax-b\Vert _2^2 \Leftrightarrow A^tAx=A^tb$$

Se $A$ ha rango $n$ (cioè se le colonne di $A$ sono vettori $n$-dimensionali indipendenti) allora $A^tA$ è simmetrica definita positiva e quindi nonè singolare.

Esiste allora, ed è unica, una soluzione $x$ - $A^tA$ che potrebbe però essere estremamente malcondizionata.