Next: Indice analitico Up: Algebra Lineare Numerica Previous: Cenno ai sistemi sovradeterminati Indice Indice analitico
Si rammenta che:
Si può altrimenti caratterizzare:
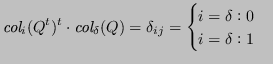
(La norma euclidea è 1).
Si assuma che
![]() , ovvero il massimo possibile.
, ovvero il massimo possibile.
Se ![]() è triangolare superiore allora
è triangolare superiore allora ![]() è anch'essa triangolare superiore.
è anch'essa triangolare superiore.
![$\displaystyle [ \textit{col}_1(A) \textit{col}_2(A) \ldots \textit{col}_n(A) ] ...
...{11} & p_{12} & \cdots & p_{1n} \\ 0 \\ 0 & 0 & \ldots & p_{n,n} \end{bmatrix} $](img1011.png)
Risultano vettori ortonormali da vettori indipendenti - il procedimento è equivalente ad applicare Gram-Schmidt sulle colonne di ![]() ).
).
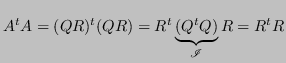
![]() è una matrice non singolare, per cui il sistema di partenza diventa equivalente a:
è una matrice non singolare, per cui il sistema di partenza diventa equivalente a:
Questo è il sistema dell'equazione normali scritto in un'altra forma.
La fattorizzazione QR è il secondo algoritmo più usato al mondo (dopo FFT).
Matteo Lisotto, Tobia Tesan - CC-BY 2.0