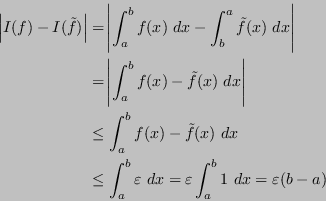Next: Formule di quadratura Up: Appunti di Calcolo Numerico Previous: Caso lineare: retta dei Indice Indice analitico
Si rammentino i teoremi fondamentali del calcolo:
Si definisce ``funzione integrale'' di ![]() la funzione
la funzione ![]() tale che:
tale che:
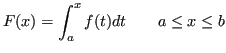
Se ![]() è limitata, allora
è limitata, allora ![]() è una funzione continua in
è una funzione continua in ![]() .
.
Se inoltre ![]() è una funzione continua in
è una funzione continua in ![]() , allora
, allora ![]() è differenziabile in tutti i punti in cui
è differenziabile in tutti i punti in cui ![]() è continua e si ha:
è continua e si ha:
cioè la ![]() risulta essere una primitiva di
risulta essere una primitiva di ![]() .
.
Sia cioè ![]() tale che:
tale che:
Se ![]() è integrabile si ha:
è integrabile si ha:
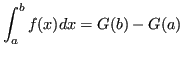
Si ricordi che:
Allora