Formule di quadratura algebriche
Le formule di quadratura algebriche utilizzano, per l'approssimazione un polinomio interpolatore.
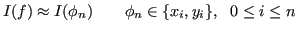
e
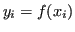
Sia
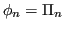 allora
allora
L'integrale definito del prodotto di Lagrange è detto peso, e il risultato è chiamato somma pesata.
Le formule di quadratura si dividono nelle seguenti famiglie:
- Formule di Newton-Cotes: utilizzano nodi equispaziati. Non sono in generale convergenti.
- Formula di Clenshaw-Curtis: utilizzano i nodi di Chebychev. Convergono per
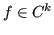 con
con 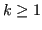 .
.
- Formule Gaussiane: richiedono una distribuzione speciale dei nodi.
Le formule algebriche sono, per costruzione, esatte (l'errore è nullo) sui polinomi di grado 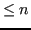 (la funzione interpolatoria è il polinomio stesso).
(la funzione interpolatoria è il polinomio stesso).
Le formule gaussiane sono esatte fino al grado 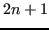 ma chiedono una scelta ``specialissima'' dei nodi di campionamento.
ma chiedono una scelta ``specialissima'' dei nodi di campionamento.
Nelle formule di Clenshaw-Curtis e in quelle Gaussiane i pesi sono positivi (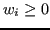 ).
).
Matteo Lisotto, Tobia Tesan - CC-BY 2.0
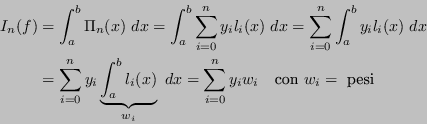
![]() ma chiedono una scelta ``specialissima'' dei nodi di campionamento.
ma chiedono una scelta ``specialissima'' dei nodi di campionamento.
![]() ).
).