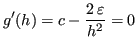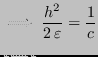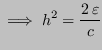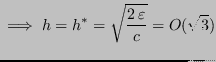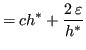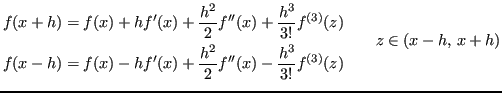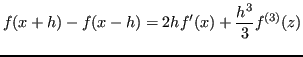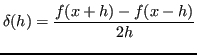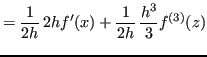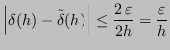Derivazione numerica
La derivazione numerica si occupa di derivare funzioni a partire da approssimazioni di esse.
Teorema 5.7
La derivazione numerica non è in generale stabile.
Vi sono due approcci principali alla derivazione numerica:
- Globale: si cerca di approssimare
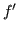 su tutto l'intervallo
su tutto l'intervallo ![$ [a,\,b]$](img574.png) tramite interpolazione spline.
tramite interpolazione spline.
- Locale: calcolo
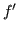 tramite rapporto incrementale su un punto.
tramite rapporto incrementale su un punto.
Per definizione di derivata, si ha:
Sia
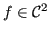 in un intorno di
in un intorno di 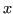 . Applicando la formula di Taylor si ha:
. Applicando la formula di Taylor si ha:
Il rapporto incrementale
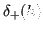 si può esprimere come:
si può esprimere come:
Sia 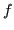 approssimata da
approssimata da 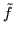 , con un errore maggiorabile con un
, con un errore maggiorabile con un
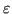 fissato:
fissato:
Si ha di conseguenza un rapporto incrementale approssimato
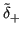 :
:
Si può analizzare la stabilità sviluppando l'espressione dell'errore:
Quindi:
Sia
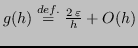 . Si noti che per
. Si noti che per 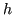 molto piccolo, l'errore diventa molto grande.
molto piccolo, l'errore diventa molto grande.
Si deve trovare
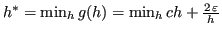 :
:
Sia quindi
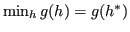 .
.
Funzioni arbitrariamente vicine possono avere derivata molto diversa.
Si può ottenere una stima migliore considerando un ordine in più nella formula di Taylor:
Calcolando il rapporto incrementale simmetrico 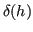 , risulta:
, risulta:
Inoltre, si vede che:
L'errore risulta:
Matteo Lisotto, Tobia Tesan - CC-BY 2.0
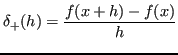
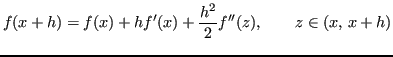
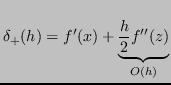
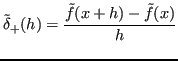
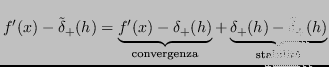
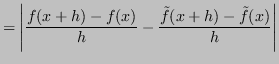
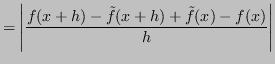
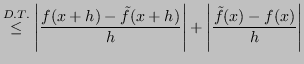
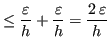
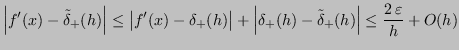
![]() . Si noti che per
. Si noti che per ![]() molto piccolo, l'errore diventa molto grande.
molto piccolo, l'errore diventa molto grande.
![]() :
: