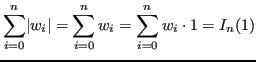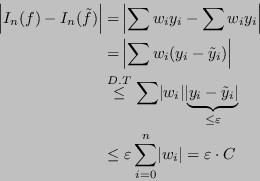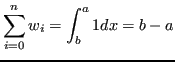Osservazione 5.1
Le formule di quadratura algebriche sono esatte su tutti i polinomi di grado
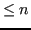
(l'interpolatoria è il polinomio stesso);
Le formule di quadratura composte sono esatte su tutti i polinomi di grado
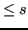
(lineari per grado
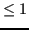
, quadratiche per grado
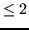
).
In generale le formule di integrazione su
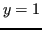
(grado
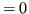
) sono esatte, pertanto
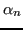
non solo è limitata, ma è addirittura costante (
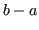
).
L'errore può quindi aumentare al massimo della lunghezza dell'intervallo.
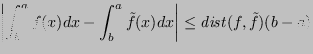
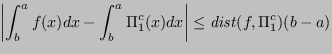
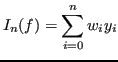
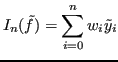
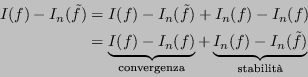
![$\displaystyle \Lambda_n = \max_{x\in[a,b]} \sum_{i=0}^n\abs{ l_i(x)} $](img770.png)