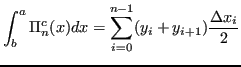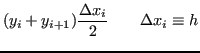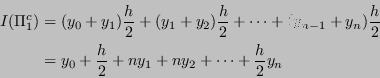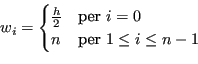Caso lineare (Formule dei trapezi)

Nelle formule dei trapezi (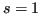$s = 1$) ogni polinomio interpolatore 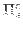$\Pi_s^c$ è una retta e l'integrale definito equivale all'area del trapezio di vertici $x_i, \ x_{i+1}, \ y_i, \ y_{i=1}$.

$$\int_b^a \Pi_n^c(x) dx = \sum_{i=0}^{n-1}(y_i+y_{i+1})\frac{\Delta x_i}{2}$$

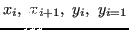Dove l'area del trapezio i-esimo è:

$$(y_i+y_{i+1})\frac{\Delta x_i}{2} \qquad \Delta x_i \equiv h$$

L'integrale approssimato risulta:

$$\begin{split} I(\Pi_1^c) &= (y_0 + y_1)\frac{h}{2} + (y_1+y_... ...&= y_0+\frac{h}{2}+ny_1+ny_2+\dots+\frac{h}{2}y_n % \end{split}$$

Nella forma di somme pesate si ha:

$$w_i = \begin{cases} \frac{h}{2} & \text{per } i = 0 \\ n & \text{per } 1 \le i \le n-1 % \end{cases}$$