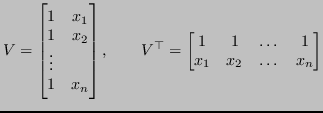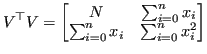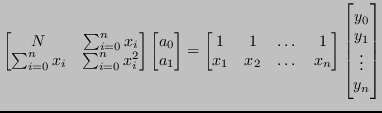Caso lineare: retta dei minimi quadrati
Con 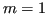 , l'insieme di punti viene approssimato da una retta. Il sistema
, l'insieme di punti viene approssimato da una retta. Il sistema
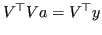 è quindi formato dalle seguenti componenti:
è quindi formato dalle seguenti componenti:
Il sistema risulta quindi:
Nel problema del minimo quadrato, si vuole trovare il vettore dei coefficenti
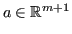 per cui
per cui
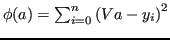 è minimo.
è minimo.
Per definizione di prodotto scalare:
Se 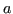 è minimo, allora
è minimo, allora
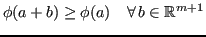 |
(6) |
Quindi, la (6) diventa:
Fissato
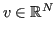 e posto
e posto
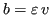 , si ha:
, si ha:
Passando al limite per
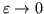 , si ha:
, si ha:
Si noti che, con 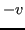 al posto di
al posto di 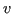 , si ha
, si ha
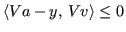 , pertanto:
, pertanto:
Matteo Lisotto, Tobia Tesan - CC-BY 2.0