Approssimazione Polinomiale dei Minimi Quadrati
L'interpolazione polinomiale di LaGrange non migliora l'interpolazione al crescere del grado. Tale inconveniente può essere superato con l'interpolazione a tratti e spline, che però poco si prestano ad estrapolare previsioni sui dati, ovvero valori di cui non si ha un campionamento.
Supponiamo di disporre di un insieme di 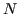 dati campione
dati campione
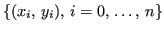 . Dato un grado
. Dato un grado 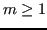 (tipicamente
(tipicamente 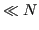 ), si vuole trovare un polinomio
), si vuole trovare un polinomio
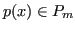 tale che:
tale che:
Trovare 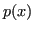 equivale a trovare un vettore di coefficenti
equivale a trovare un vettore di coefficenti
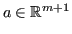 tale che
tale che
Quando 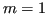 , si parla di retta dei minimi quadrati o retta di regressione.
, si parla di retta dei minimi quadrati o retta di regressione.
Sia
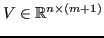 matrice rettangolare tale che
matrice rettangolare tale che
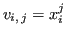 , e sia
, e sia
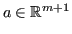 il vettore colonna dei coefficenti:
il vettore colonna dei coefficenti:
Come si può dimostrare, tale problema ha un'unica soluzione, calcolabile risolvendo il sistema lineare
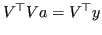 .
.
Subsections
Matteo Lisotto, Tobia Tesan - CC-BY 2.0
![]() dati campione
dati campione
![]() . Dato un grado
. Dato un grado ![]() (tipicamente
(tipicamente ![]() ), si vuole trovare un polinomio
), si vuole trovare un polinomio
![]() tale che:
tale che:
![$\displaystyle \sum_{i=0}^{n} \left[ p(x) - y_i \right]^2 \leq \sum_{i=0}^{n} \left[ q(x) - y_i \right]^2, \qquad \forall q \in P_m
$](img687.png)
![$\displaystyle a = \min_{v \in \mathbb{R}^{m+1}} \sum_{i=0}^{n} \left[ (v_0 + v_1 x_i + v_2 x_i^2 + \dots + v_m x_i^m) - y_i \right]^2
$](img689.png)
![]() matrice rettangolare tale che
matrice rettangolare tale che
![]() , e sia
, e sia
![]() il vettore colonna dei coefficenti:
il vettore colonna dei coefficenti: