Interpolazione Spline

Utilizzando l'interpolazione polinomiale a tratti si ha che, nei raccordi, in generale, non è nemmeno possibile derivare $\Pi_S^C$. Si ha una moltitudine di punti angolosi e ciò è specialmente indesiderabile nella grafica.

Per ovviare a questo problema si usa l'interpolazione spline⁴.

Si cercano funzioni interpolanti lisce, senza punti angolosi, ossia:

Definizione 4.10 (Interpolante Spline)   Si chiama interpolante spline una funzione $S_k(x) \in C^{k-1}[a,b]$ tale che:

1. $S_k(x) \big\vert _{I_i} \in P_k$
2. $S_k(x_i) = y_i,\qquad 0 \le i \le n$
3. $S_k^{(j)}(x_i^+) = S_k^{(j)}(x_i^-)\qquad 0 \le i \le n-1 \quad 0 \le j \le k-1$

Distinguiamo le funzioni spline in base al loro grado $k$; con $k=1$ avremo spline lineari, mentre con $k=3$ avremo spline cubiche.

Le spline cubiche sono il tipo più usato nella pratica:

Definizione 4.11 (Interpolante spline cubica)   Si chiama interpolante spline una funzione $S_k(x) \in C^{k-1}[a,b]$ con $k=3$, dunque:

1. $\left.S_3\right\vert _I \in P_3$
2. $S_3(x_i) = y_i \qquad 0 \le i \le n$
3. $S_3 \in C^2[a,b]$

Osservazione 4.2   Si osservi che $\left.S_3\right\vert _I \in P_3$ equivale a dire che $S_3\vert_I = a_{0i} + a_{1i}x + a_{2i}x^2 + a_{3i}x^3$ con $0 \le i \le n-1$: si hanno ossia $n$ intervallini, ciascuno dei quali ``vede'' quattro incognite.

Osservazione 4.3   $S_3(x_i) = y_i$ implica trivialmente che agli estremi deve valere $S_3(x_0) = y_0, S_3(x_n) = y_n$.

Osservazione 4.4   Inoltre, poichè $S_3 \in C^2[a,b]$

$$\begin{cases} S_3(x_i^+) = S_3(x_i^-), \quad 1 \le i \le n-1... ...x_i^+) = S_3'(x_i^-) \\ S_3''(x_1^+) = S_3''(x^-) \end{cases}$$

Osservazione 4.5   Il sistema che risulta dei vincoli è sottodimensionato e dunque singolare.

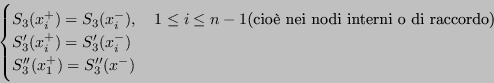
Mettendo a sistema i vincoli si vede che si hanno $4n$ incognite (4 incognite $a_{0..3}$ per ogni polinomio $S_{3, i}$ e $n$ polinomi).

Si hanno inoltre $4n-2$ equazioni: $n+1$ equazioni per le condizioni di interpolazione, $n-1$ equazioni per la continuità di $S_3(x)$ su $n-1$ nodi interni e $2(n-1)$ equazioni per la continuità della derivata prima e seconda sui nodi interni.

È possibile ottenere un sistema non singolare aggiungendo arbitrariamente, ad esempio:

$$S_3''(x_0) = 0\qquad S_3''(x_n) = 0$$

La soluzione del sistema risultante permette di determinare la funzione spline cubica interpolatoria.