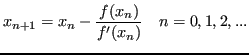Metodo di Newton

Il metodo di Newton si basa sull'idea di sfruttare, come successiva approssimazione della radice, il punto di intersezione della retta tangente alla funzione del punto $(x_0, f(x_0))$ con l'asse delle ascisse, considerando $x_0$ un'approssimazione iniziale ``sufficientemente buona'' (ottenuta per ispezione grafica o con un paio di iterazioni del metodo di bisezione).

L'idea fondamentale è che, anche in una funzione non lineare, la tangente in un punto possa ``puntare'' all'incirca verso lo zero. Banalmente allora occorre che $f \in C'$.

Poichè l'equazione della retta tangente al punto $(x_0, f(x_0))$ è:

$$y = f(x_0) + f'(x_0)(x-x_0)$$

L'equazione dell'intersezione della retta con l'asse $x$ si ottiene mettendo a sistema a risolvendo:

$$\begin{cases} y = f(x_0) + f'(x_0)(x-x_0) \\ y = 0 \end{cases}$$

$$x = x_0 - \frac{f(x_0)}{f'(x_0)}$$

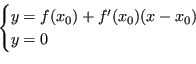
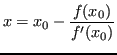
Più in generale si costruirà una successione $\{x_n\}$ t.c.:

$$x_{n+1} = x_n - \frac{f(x_n)}{f'(x_n)} \quad n=0,1,2,...$$