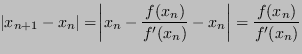Stima dell'errore

Stimare l'errore con il passo 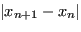$\abs{x_{n+1}-x_n}$ è pericoloso in generale, ma nel caso del metodo di Newton porta a buoni risultati per costruzione stessa del metodo:

$$\abs{x_{n+1}-x_{n}} = \abs{x_n-\frac{f(x_n)}{f'(x_n)}-x_n} = \frac{f(x_n)}{f'(x_n)}$$

Si noti che il passo 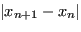$\abs{x_{n+1}-x_n}$ assume la forma di un residuo pesato. L'arresto del metodo, fissata una tolleranza 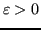$\varepsilon > 0$, avverrà quando:

$$\abs{x_{n+1}-x_n} < \varepsilon$$