Next: Confronto con il metodo Up: Metodo di Newton Previous: Convergenza del Metodo di Indice Indice analitico
Sia ![]() una successione convergente a
una successione convergente a ![]() e sia
e sia
![]() l'errore al passo
l'errore al passo ![]() .
.
Se
![]() t.c.:
t.c.:
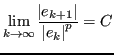
Allora ![]() è chiamato ordine di convergenza della successione e
è chiamato ordine di convergenza della successione e ![]() è la costante asintotica di errore.
è la costante asintotica di errore.
Per ![]() la convergenza si dice lineare, per
la convergenza si dice lineare, per ![]() si dice quadratica.
si dice quadratica.