Next: Ordine di convergenza del Up: Metodo di Newton Previous: Metodo di Newton Indice Indice analitico
La convergenza del metodo di Newton non è sempre garantita.
Esistono diversi teoremi che sotto particolari ipotesi permettono di provarne la convergenza.
Alcuni sono detti di convergenza locale e dicono che se
![]() intorno di
intorno di ![]() sufficientemente piccolo allora il metodo converge.
Altri sono detti di convergenza globale e dicono che se
sufficientemente piccolo allora il metodo converge.
Altri sono detti di convergenza globale e dicono che se ![]() appartiene a un ben definito intorno
appartiene a un ben definito intorno
![]() di
di ![]() allora il metodo converge.
allora il metodo converge.
La funzione è ossia strettamente concava o strettamente convessa.
La funzione e la derivata seconda hanno ossia segni concordi.
Sotto queste ipotesi di convergenza globale, il metodo di Newton è ben definito e si ha
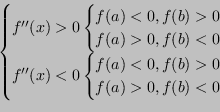
Si considererà il caso
![]() ,
,
![]() (gli altri casi sono simmetrici).
(gli altri casi sono simmetrici).
Se ![]() e
e
![]() allora
allora ![]() in un intorno sinistro sufficientemente piccolo di
in un intorno sinistro sufficientemente piccolo di ![]() .
.
Se ![]() in un intorno sinistro sufficientemente piccolo di
in un intorno sinistro sufficientemente piccolo di ![]() , poichè
, poichè ![]() allora
allora ![]() in
in ![]() .
.
Allora in ![]()
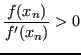
Quindi
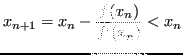
![]()
Si considererà ancora il caso
![]() ,
,
![]() (gli altri casi sono simmetrici).
(gli altri casi sono simmetrici).
Poichè ![]() l'intersezione della tangente con l'asse delle
l'intersezione della tangente con l'asse delle ![]() è sempre a destra dell'intersezione della
è sempre a destra dell'intersezione della ![]() con l'asse medesima, dunque
con l'asse medesima, dunque ![]() è inferiormente limitata da
è inferiormente limitata da ![]() :
:
![]() .
.
Per questo e poichè ![]() è decrescente è vero:
è decrescente è vero:
![]() .
.
Posto allora che:
Poichè ![]() è strettamente decrescente:
è strettamente decrescente:
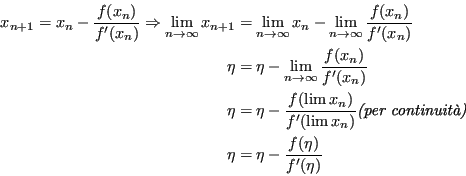
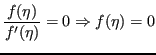
Allora ![]() è soluzione, e per unicità:
è soluzione, e per unicità:
![]()
Allora
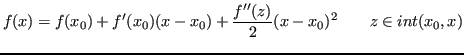
Pertanto si può esprimere ![]() come
come
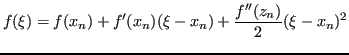
Dunque, manipolando algebricamente:
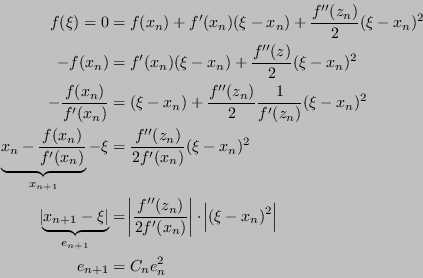
Si ricordi a questo punto il teorema di Weierstrass:
Pertanto,
![]() ha un massimo assoluto in
ha un massimo assoluto in
![]() e
e
![]() ha un minimo assoluto in
ha un minimo assoluto in ![]() :
:
![\begin{displaymath}\begin{split}
\vert f''(z_n)\vert& \leq \max_{x \in [a,b]} \...
...rt& \geq \min_{x \in [a,b]} \vert f'(x)\vert = m > 0\end{split}\end{displaymath}](img428.png)
Dunque, scelto
![]() :
:
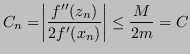
E segue dunque:
![]()
Matteo Lisotto, Tobia Tesan - CC-BY 2.0