Interpolazione polinomiale a tratti

L'idea di base dell'interpolazione polinomiale a tratti consiste nel prendere un $\Pi$ interpolante costituito da un polinomio per ciascuna coppia di punti consecutivi.

Dato un intervallo $[a, b]$, si procede dunque a suddividerlo in una serie di $n$ intervallini $[x_i, x_{i+1}]$ tali che:

$$x_i = a + i\cdot \qquad h = \frac{b-a}{n} \qquad 0 \le i \le n$$

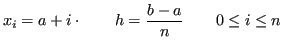
Il caso più semplice è quello con grado 1, ovvero l'interpolazione lineare composita.

In tal caso $\Pi_1^C(x)$ è lineare in $[x_i, x_{i+1}]$ e la funzione ottenuta è una spezzata lineare a tratti nonchè continua.

In questo caso $\Pi_2^C(x)$ consiste in pezzi di parabola ``incollati'' insieme.

Il $\Pi$ ottenuto è una funzione quadratica a tratti.

Per tre punti non allineati passa una ed una sola parabola, dunque bisogna organizzare i punti a ``pacchetti'' di 3 - ovvero, organizzare gli intervallini a ``pacchetti'' di 2.

Occorre dunque scegliere $n=2k$.

Più in generale vale:

Lemma 4.15   Con $\Pi_S^C(x)$ di grado $S$ il numero di punti $n$ deve essere multiplo di $S$, avendo:

$$x_i = \lbrace (x_0, x_1, \ldots, x_s), (x_{S_1}, x_{S_1+1}, \ldots, x_{2s}), (x_{n-s}, x_{n-s+1}, \ldots, x_n) \rbrace$$