Next: Stabilità dell'interpolazione polinomiale a Up: Interpolazione polinomiale a tratti Previous: Interpolazione polinomiale a tratti Indice Indice analitico
Sia
![]() , con
, con ![]() multiplo di
multiplo di ![]() , allora:
, allora:
Si rammenti che l'errore in forma di Lagrange (vedi 3) è:
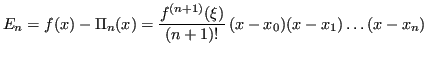
Allora, con ![]() :
:
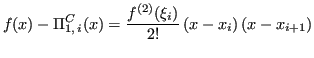 |
|
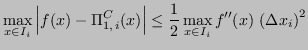 |
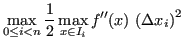 |
 |
|
Matteo Lisotto, Tobia Tesan - CC-BY 2.0