Interpolazione polinomiale
Si immagini di disporre di:
Si vuole ricercare un cosiddetto polinomio interpolatore
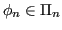 interpolante la
interpolante la 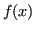 sulle ascisse
sulle ascisse
![$ x_i \in [a,b]$](img523.png) ,
, 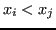 se
se
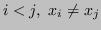 se
se 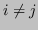 , tale che:
, tale che:
Teorema 4.1 (Esistenza di un unico polinomio interpolatore)
Per ogni insieme di coppie
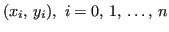 , con nodi
, con nodi 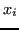 distinti fra loro,
distinti fra loro,
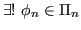 tale che
tale che
$&sstarf#star;$ Dimostrazione 4.1 (Unicità del polinomio interpolatore)
Si supponga per assurdo che che esistano due polinomi
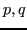
di grado
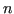
, entrambi interpolatori per i punti
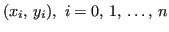
. Allora,
Per il teorema fondamentale dell'algebra 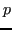 e
e 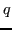 hanno esattamente
hanno esattamente 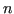 zeri complessi e al più
zeri complessi e al più 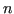 zeri reali.
zeri reali.
Si consideri il polinomio 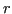 differenza tra i due:
differenza tra i due:
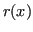
è di grado
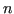
, in quanto differenza di due polinomi di grado
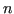
, e ha
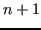
zeri, poichè
Ma per il teorema fondamentale
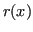
non può esistere, dunque:

$&sstarf#star;$ Dimostrazione 4.2 (Esistenza del polinomio interpolatore)
Si dimostra l'esistenza di tale polinomio mostrando che è sempre possibile costruirne uno.
Il polinomio interpolatore è nella forma:
Le condizioni di interpolazione sono rappresentabili da un sistema di
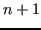
equazioni (una per ogni campione) e
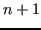
incognite
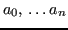
, che costituiscono i coefficienti del polinomio.
Il sistema è nella forma
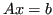
, con
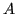
matrice di Vandermonde:
Definizione 4.6 (Matrice di Vandermonde)
Una matrice di Vandermonde è una matrice in cui gli elementi delle righe costituiscono una progressione geometrica, ovvero:
Il determinante di 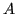 può essere espresso come:
può essere espresso come:
Se
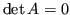
, la matrice è singolare e ha infinite soluzioni. Per ipotesi, però, i nodi
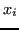
sono distinti tra loro, quindi
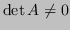
, la matrice è invertibile e il sistema ammette soluzione unica
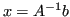
.

Dimostrazione 4.2
Un'ulteriore dimostrazione di esistenza consiste nel costruire il polinomio nella cosiddetta
forma di Lagrange. Siano
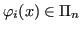
polinomi definiti come segue:
Tali particolari polinomi sono definiti
polinomi caratteristici di Lagrange. Si noti che il loro comportamento è analogo al
delta di Kronecker
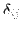
:
Dai polinomi
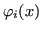
si ottiene
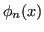
per sovrapposizione degli effetti:
Tale polinomio soddisfa le condizioni di interpolarizzazione ed è pertanto un polinomio interpolatore, espresso in
forma di Lagrange.
Definizione 4.7 (Errore di interpolazione)
Si chiama errore di interpolazione
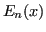
la distanza tra una funzione
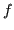
e il polinomio interpolatore
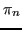
al passo
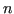
:
Dimostrazione 4.3
Si vuole dimostrare la (
3) per ogni
![$ x \in [a,\,b]$](img564.png)
. Se
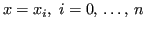
, la tesi è triviale.
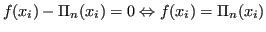
per definizione di
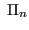
Sia
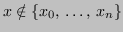
fissato, e sia
![$ z \in [a,\,b]$](img570.png)
. Definiamo
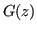
come:
dove
Si ricordi allora il teorema di Rolle:
I nodi 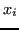 e
e 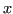 suddividono l'intervallo
suddividono l'intervallo ![$ [a,\,b]$](img574.png) in
in 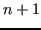 intervalli, dove G(z) si annulla trivialmente. Allora, per il teorema di Rolle, in ogni intervallo
intervalli, dove G(z) si annulla trivialmente. Allora, per il teorema di Rolle, in ogni intervallo 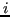 -esimo
-esimo
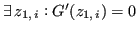 . Analogamente, i punti
. Analogamente, i punti 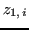 suddividono l'intervallo
suddividono l'intervallo
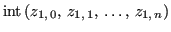 in
in 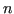 intervalli dove
intervalli dove
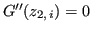 . Reiterando Rolle, si ottiene:
. Reiterando Rolle, si ottiene:
Per la linearità dell'operatore di derivazione, si ha:
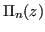
ha grado
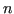
, pertanto
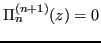
.
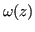
ha termine di grado massimo
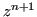
, quindi
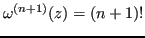
. Quindi, si ha

Lemma 4.2 (Maggiorazione dell'errore)
Dove 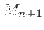 è la massima derivata
è la massima derivata 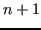 -esima.
-esima.
Lemma 4.3 (Convergenza)
Poichè
Se
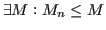
Esempio 4.1
Si consideri
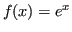
. Si ha che
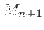
è limitata dalla costante
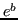
, pertanto
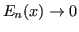
.
Tale stima vale per ogni distribuzione dei nodi.
Lemma 4.4
Come si può dimostrare, in caso di distribuzione esclusivamente equidistante, l'errore è inoltre maggiorabile come segue:
Lemma 4.5
In generale, con l'interpolazione polinomiale, non c'è convergenza uniforme (neppure convergenza puntuale).
Dimostrazione 4.4 (Esempio di Runge)
Il cosiddetto esempio di Runge vale come controesempio di
4.5.
Sia
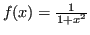 e
e
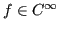
Eseguiamo un campionamento a passo costante, ovvero prendiamo dei punti equispaziati tra loro. Notiamo che più aumentiamo di grado il nostro polinomio interpolatore più le oscillazioni agli estremi aumentano. Questo problema è dovuto alla scelta di campionamento a passo costante. Sicuramente non c'è convergenza uniforme e, vicino agli estremi non c'è neppure quella puntuale.
Matteo Lisotto, Tobia Tesan - CC-BY 2.0
![]() interpolante la
interpolante la ![]() sulle ascisse
sulle ascisse
![]() ,
, ![]() se
se
![]() se
se ![]() , tale che:
, tale che:
![]() e
e ![]() hanno esattamente
hanno esattamente ![]() zeri complessi e al più
zeri complessi e al più ![]() zeri reali.
zeri reali.
![]() differenza tra i due:
differenza tra i due:
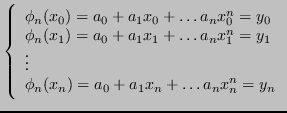
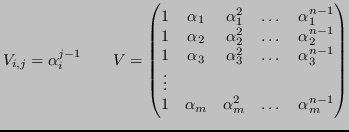
![]() può essere espresso come:
può essere espresso come:
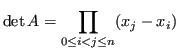
![]()
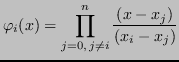
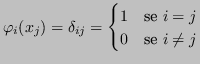
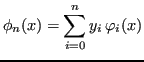

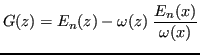
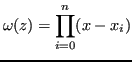
![]() e
e ![]() suddividono l'intervallo
suddividono l'intervallo ![]() in
in ![]() intervalli, dove G(z) si annulla trivialmente. Allora, per il teorema di Rolle, in ogni intervallo
intervalli, dove G(z) si annulla trivialmente. Allora, per il teorema di Rolle, in ogni intervallo ![]() -esimo
-esimo
![]() . Analogamente, i punti
. Analogamente, i punti ![]() suddividono l'intervallo
suddividono l'intervallo
![]() in
in ![]() intervalli dove
intervalli dove
![]() . Reiterando Rolle, si ottiene:
. Reiterando Rolle, si ottiene:
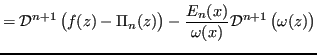
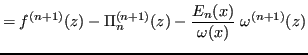
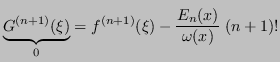
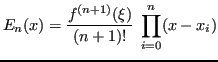
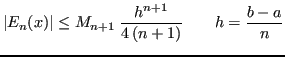
![]() e
e
![]()