Next: Interpolazione polinomiale Up: Approssimazione di funzioni e Previous: Approssimazione di funzioni e Indice Indice analitico
La convergenza uniforme è indipendente dal valore di ![]() e pertanto un concetto più forte di quella puntuale.
e pertanto un concetto più forte di quella puntuale.
Ogni funzione ![]() è nulla per
è nulla per
![]() . La successione converge puntualmente a
. La successione converge puntualmente a ![]() , poichè, fissato un certo
, poichè, fissato un certo ![]() , si riesce sempre a trovare un numero
, si riesce sempre a trovare un numero ![]() tale che:
tale che:
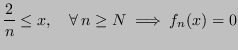
Matteo Lisotto, Tobia Tesan - CC-BY 2.0