Stabilità dell'interpolazione polinomiale
Posto
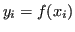 , spesso si avranno a disposizione dei valori approssimati
, spesso si avranno a disposizione dei valori approssimati
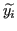 invece di
invece di 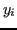 , dovuto ad esempio all'errore commesso dal calcolatore nel valutare
, dovuto ad esempio all'errore commesso dal calcolatore nel valutare 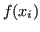 .
.
Si supponga di poter stimare un valore massimo
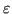 di tale errore sui dati:
di tale errore sui dati:
Si indicherà con
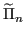 il polinomio interpolatore calcolato con
il polinomio interpolatore calcolato con
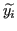 .
.
Allora:
Sapendo che
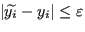 e applicando la disuguaglianza triangolare, si ha:
e applicando la disuguaglianza triangolare, si ha:
Il valore 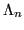 è chiamato costante di Lebesgue. Allora,
è chiamato costante di Lebesgue. Allora,
Lemma 4.10
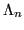
dipende unicamente dal prodotto di LaGrange, e quindi dai nodi.
Inoltre, si ha che:
Lemma 4.11
Su nodi equidistanti,
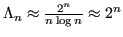
Lemma 4.12
Su nodi di Chebyshev,
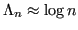
.
Di conseguenza:
Lemma 4.13
Con distribuzione equidistante, l'interpolazione polinomiale reagisce in modo instabile alle perturbazioni sul campionamento della funzione da interpolare
Lemma 4.14
L'interpolazione polinomiale risulta sostanzialmente stabile con la distribuzione di Chebychev.
Matteo Lisotto, Tobia Tesan - CC-BY 2.0
![]() di tale errore sui dati:
di tale errore sui dati:
![]() il polinomio interpolatore calcolato con
il polinomio interpolatore calcolato con
![]() .
.
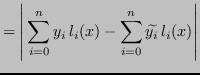
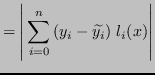
![]() e applicando la disuguaglianza triangolare, si ha:
e applicando la disuguaglianza triangolare, si ha:
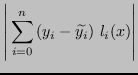
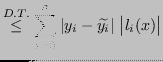
![$\displaystyle \leq \varepsilon \underbrace{\max_{x \in [a,\,b]} \sum_{i=0}^{n} \left\vert l_i(x) \right\vert}_{\Lambda_n}$](img630.png)