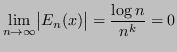Nodi di Chebychev
Definizione 4.8 (Nodi di Chebychev)
Siano
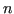
angoli equispaziati compresi tra
0 e
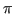
:
Si chiamano nodi di Chebychev l'insieme delle loro proiezioni sulla circonferenza:
Su un intervallo ![$ [a, b]$](img305.png) :
:
Osservazione 4.1
È apparente che in prossimità degli estremi i nodi si addensano.
Definizione 4.9 (Polinomio interpolatore di Chebychev)
È possibile scrivere il polinomio interpolatore in forma di Lagrange nel seguente modo, ponendo
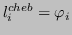
:
Teorema 4.4 (Esistenza e unicità del polinomio interpolatore di Chebychev)
Come banale conseguenza dell'essere in forma di Lagrange, il polinomio interpolatore esiste ed è unico.
Teorema 4.5 (Convergenza dell'interpolazione con nodi di Chebychev)
Se
![$ f \in C^K[a,b], K \ge 1$](img614.png) l'interpolazione con i nodi di Chebychev converge.
l'interpolazione con i nodi di Chebychev converge.
Lemma 4.8
La convergenza con i nodi di Chebychev è uniforme.
Lemma 4.9
Più volte la
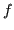
è derivabile, più sarà veloce la sua convergenza.
Dimostrazione 4.5
Se
![$ f \in C^K[a,b], K \ge 1$](img614.png)
:
Poichè 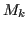 è costante:
è costante:

Matteo Lisotto, Tobia Tesan - CC-BY 2.0
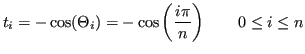
![]() :
:
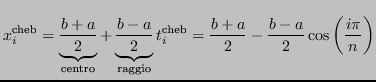
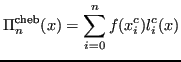
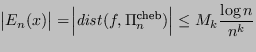
![]() è costante:
è costante: