Norma di matrici
Definizione 6.15 (Applicazione lineare)
Sia
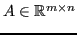
. Allora è applicazione lineare
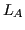
:
t.c.:
Definizione 6.16 (Norma di matrice)
Sia
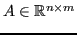
,fissata una norma vettoriale, si definisce la norma
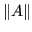
come:
Da tale definizione si ricava una proprietà fondamentale delle norme matriciali:
Teorema 6.4 (Proprietà fondamentale)
Sia
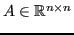 ,
,
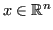 :
:
Dimostrazione 6.1
Triviale: significa che, per
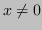
,
In pratica:
Quindi

Definizione 6.17
La distanza tra due matrici è la norma della differenza:
Esempio 6.1
Con norma infinito la norma matriciale è:
Esempio 6.2
Con norma euclidea la norma matriciale è:
dove
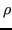
è il raggio spettrale.
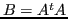 simmetrico (autovalore reale) e ha autovalori
simmetrico (autovalore reale) e ha autovalori 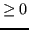 .
.
Matteo Lisotto, Tobia Tesan - CC-BY 2.0
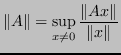

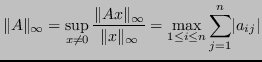
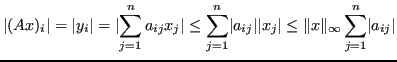
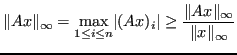
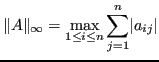
![]() simmetrico (autovalore reale) e ha autovalori
simmetrico (autovalore reale) e ha autovalori ![]() .
.