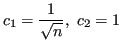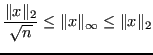Definizione 6.6 (Norma vettoriale)
Una norma su uno spazio vettoriale reale
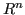
è una funzione
tale che
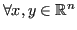 :
:
-
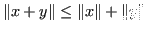 (D.T.)
(D.T.)
-
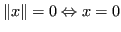
-
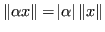
Definizione 6.7 (Distanza indotta da una norma)
Per definizione la distanza è simmetrica
Definizione 6.8 (Norma uno)
Con
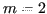
trivialmente
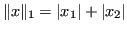
Definizione 6.9 (Norma due o Euclidea)
Definizione 6.10 (2-distanza)
Definizione 6.11 (Norma infinito)
Definizione 6.12 (
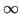
-distanza)
Si consideri un intorno
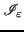 di
di 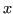 con raggio
con raggio
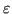 rispetto a una distanza:
rispetto a una distanza:
Visivamente, possiamo immaginare:
- Un intorno in norma due come cerchi di raggio
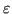
- Un intorno in norma infinito come quadratini di lato
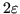
- Un intorno in norma uno come rombi di lato
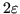
Definizione 6.13 (Norme equivalenti)
Siano due norme
Esse si dicono equivalenti se:
Teorema 6.1
In uno spazio vettoriale finito-dimensionale tutte le norme sono equivalenti
Definizione 6.14 (Limite di una successione)
Sia una successione
allora
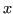 è limite della successione.
è limite della successione.
Teorema 6.3 (Proprietà fondamentale delle successioni)
Una successione è convergente se e solo se ogni sua sottosuccessione è convergente.
Ciò implica la convergenza elemento per elemento.
Matteo Lisotto, Tobia Tesan - CC-BY 2.0
![]() :
:
![]() di
di ![]() con raggio
con raggio
![]() rispetto a una distanza:
rispetto a una distanza:
![]() è limite della successione.
è limite della successione.