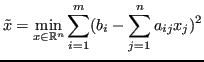Cenni di Algebra Lineare
Definizione 6.1 (Sistema lineare)
Un
sistema lineare è un sistema nella forma
Dove
Definizione 6.2 (Sistema quadrato)
Un
sistema quadrato è un
sistema lineare con
Definizione 6.3 (Sistema sovradeterminato)
Un
sistema sovradeterminato è un sistema con
Un sistema sovradeterminato possiede più equazioni che incognite - ovvero, ci sono ``troppi vincoli''.
Per questo in generale non esiste una soluzione che soddisfi il sistema.
Si può però cercare una soluzione approssimata, che minimizzi la distanza rispetto ai vincoli:
Definizione 6.4 (Soluzione nel senso dei minimi quadrati)
Una soluzione nel senso dei minimi quadrati di un sistema
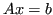
è una

tale che
Definizione 6.5 (Sistema sottodeterminato)
Se
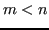
, il sistema è sottodeterminato.
Ha in genere infinite soluzioni.
Esistono una serie di approcci alla soluzione dei sistemi lineari, in generale riconducibili a due famiglie:
- Metodi diretti, ovvero metodi in cui la soluzione viene calcolata dopo un numero finito di passi (ad es. il Metodo di Eliminazione di Gauss)
- Metodi iterativi, in cui la soluzione si ottiene in un numero teoricamente infinito di passi.
In essi si cerca una successione
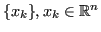 tale che
tale che
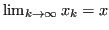 , con
, con 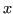 soluzione del sistema, e dunque.
Si tratta di metodi perlopiù costruiti ad hoc rispetto a un determinato problema che costituiscono attivo campo di ricerca.
soluzione del sistema, e dunque.
Si tratta di metodi perlopiù costruiti ad hoc rispetto a un determinato problema che costituiscono attivo campo di ricerca.
Subsections
Matteo Lisotto, Tobia Tesan - CC-BY 2.0