Next: Operazioni con numeri macchina Up: I numeri macchina Previous: Funzione floating Indice Indice analitico
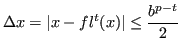
Per definizione, è possibile scrivere:
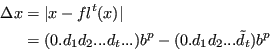
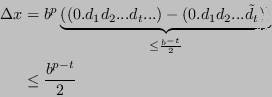
![]()
L'errore dipende da ![]() .
Si nota che se
.
Si nota che se ![]() l'errore aumenta mentre se
l'errore aumenta mentre se ![]() l'errore diminuisce.
Questo è desiderabile, poichè mantiene l'errore relativo costante.
l'errore diminuisce.
Questo è desiderabile, poichè mantiene l'errore relativo costante.
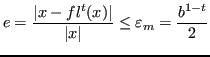
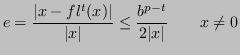
Allora, per ![]() fissato:
fissato:
quindi:
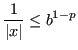
Segue:
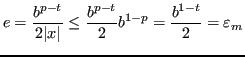
Matteo Lisotto, Tobia Tesan - CC-BY 2.0