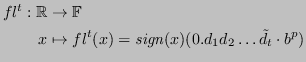Funzione floating

In quanto 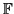$\mathbb{F}$ non può rappresentare i numeri irrazionali e ha un numero finito di elementi, è necessario definire una funzione 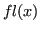$fl(x)$, detta funzione floating che associ ad ogni numero reale 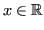$x\in\mathbb{R}$ un corrispondente rappresentante in 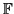$\mathbb{F}$ tale che

$$x \approx \mu = fl^t(x) \qquad x \in \mathbb{R}, \mu \in \mathbb{F}$$

Definizione 2.10 (Funzione floating)  

$$\begin{aligned} fl^t : \mathbb{R}& \to \mathbb{F}\\ x & \mapsto fl^t(x) = \mathit{sign}(x)(0.d_1 d_2 \ldots \tilde{d}_t \cdot b^p ) \end{aligned}$$