Next: Troncamento di un numero Up: Fondamenti del Calcolo Numerico Previous: L'errore relativo Indice Indice analitico

La rappresentazione può essere riscritta come:
Poichè
![]() vale:
vale:
È noto:
Allora:
È nota la seguente proprietà delle serie geometriche:
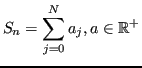
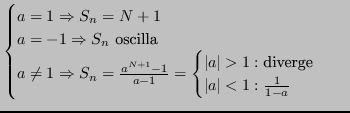
Allora, poichè
![]()
![]()