Next: Cenni su risoluzione sistemi Up: Soluzione approssimata di sistemi Previous: Soluzione approssimata di sistemi Indice Indice analitico
Si consideri:
Si supponga ora che il termine noto sia tale solo in una forma approssimata ![]() .
Ci si troverebbe dunque in realtà a risolvere:
.
Ci si troverebbe dunque in realtà a risolvere:
È possibile scrivere l'errore sul risultato come:
Interessa naturalmente sapere in che modo l'errore sul termine noto ![]() influenzi l'errore sul risultato
influenzi l'errore sul risultato ![]() .
.
Può succedere che ![]() sia molto grande.
In questo caso si parla di sistemi malcondizionati, ovvero di instabilità intrinseca del problema: la risoluzione di siffatti sistemi interessa fino a un certo punto.
sia molto grande.
In questo caso si parla di sistemi malcondizionati, ovvero di instabilità intrinseca del problema: la risoluzione di siffatti sistemi interessa fino a un certo punto.
Allora:
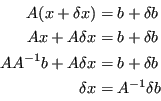
Dunque fissata una norma ![]() è possibile scrivere:
è possibile scrivere:
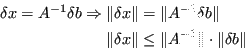
Ora, poichè
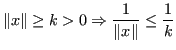
Dunque:
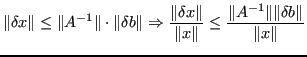
Poichè inoltre
![]() :
:
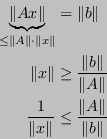
Sostituendo:
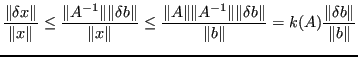
![]()
Si consideri il sistema
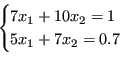
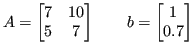
Sia ![]() il vettore dei dati perturbati:
il vettore dei dati perturbati:
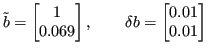
Scelta come norma la norma infinito si ottiene:
L'errore sul termine noto è il seguente:
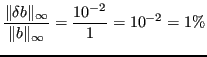
Si calcola allora la soluzione:
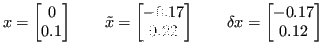
Le norme sono le seguenti:
Si ottiene un'errore sulla soluzione pari a:
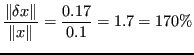
Calcolando ![]() si ha:
si ha:
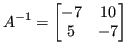
L'indice di condizionamento è:
La soluzione è quindi inaccettabile.
Matteo Lisotto, Tobia Tesan - CC-BY 2.0