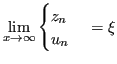Next: Vantaggi e svantaggi del Up: Criteri di Arresto Previous: Test di arresto basato Indice Indice analitico
Se non si hanno informazioni su ![]() (il calcolo di
(il calcolo di ![]() è ridotto ad una black box) è possibile usare un test empirico.
è ridotto ad una black box) è possibile usare un test empirico.
Non essendo possibile conoscere ![]() non si può applicare direttamente:
non si può applicare direttamente:
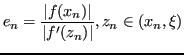
È possibile però approssimare ![]() :
:
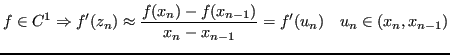
Se ![]() è continua:
è continua:
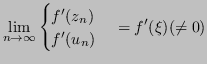
Infatti
![]() , e poiche
, e poiche
![]() e
e
![]() per il teorema dei Carabinieri:
per il teorema dei Carabinieri: