Next: Test di arresto in Up: Criteri di Arresto Previous: Arresto per stima a Indice Indice analitico
Si consideri l'equazione:
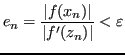
Se si conosce ![]() è possibile scegliere una costante
è possibile scegliere una costante ![]() predeterminata t.c.
predeterminata t.c.
![]() .
.
Allora l'errore è così maggiorato:
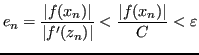
L'arresto può avvenire dunque quando
La funzione ha una soluzione ![]() in
in ![]() .
.
Si osserva che ![]() ,
, ![]() , dunque è possibile scegliere
, dunque è possibile scegliere
![]() .
.
Poichè
![]() ,
,
![]() .
.
Dunque:
Allora la scelta di ![]() garantisce che
garantisce che
![]() in
in ![]() e:
e:
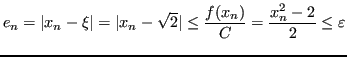
Una volta scelto un
![]() sarà dunque sufficiente arrestare il calcolo quando
sarà dunque sufficiente arrestare il calcolo quando
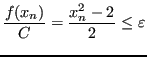
Si avrà così la certezza di avere un'approssimazione di ![]() con errore non superiore a
con errore non superiore a
![]() .
.
Matteo Lisotto, Tobia Tesan - CC-BY 2.0