Arresto per stima a posteriori tramite residuo pesato

Una stima a posteriori è una stima dell'errore eseguita durante il processo di calcolo.

Ingenuamente, può essere invogliante maggiorare il modulo del residuo con un $\varepsilon$ scelto:

$$\lvert f(x_n) \rvert < \varepsilon$$

Non è in generale una buona idea: se la funzione è molto piatta in prossimità di $\xi$ la condizione può essere soddisfatta anche in un punto molto distante da $\xi$ causando una sottostima dell'errore.

Può accadere anche il contrario: una buona approssimazione di $\xi$ può non soddisfare la condizione (se la funzione è molto pendente in prossimità della radice) - si avrebbe una sovrastima dell'errore.

La stima tramite il residuo pesato è una stima a posteriori, ovvero calcolata all'interno del processo di calcolo.

Poggia sui seguenti, noti, teoremi dell'Analisi:

Teorema 3.10   Teorema del valor medio

$$f \in C[c,d],\quad \exists f' \in (\alpha, \beta) \Rightarrow \exists z \in (c,d) : f'(z) = \frac{f(c)-f(d)}{c-d}$$

Teorema 3.11   Teorema della permanenza del segno

$$\{ a_n \} \to a_0 > 0 : \exists N : a_n > 0 : \forall n > N$$

Assumendo $f \in \mathcal{C}^1$ (continua e derivabile con derivata prima continua) e $f'(\xi) = 0$ (zero semplice), per la permanenza del segno di $f'$ si può affermare che esiste un intorno in cui $f'(x_n)$ è $\neq 0$:

$$\exists N : f'(x) \neq 0, \; \forall x \in (x_n, \xi),\;n > N$$

Possiamo applicare il teorema del valore medio all'intervallo $(x_n, \xi)$ per poter affermare, per qualche $z_n \in (x_n, \xi)$:

$$\frac{f(x_n) - \overbrace{f(\xi)}^{0}}{x_n - \xi} = \frac{f(x_n)}{x_n - \xi} = f'(z_n)$$

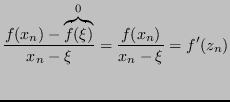
Allora, algebricamente:

$$\begin{split} f(x_n)& = f'(z_n)(x_n-\xi) \\ \Rightarrow e_n... ...\frac{\lvert f(x_n) \rvert}{\lvert f'(z_n) \rvert } \end{split}$$

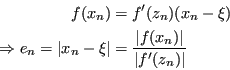
Allora è sufficiente arrestare il calcolo quando:

$$e_n = \frac{\lvert f(x_n) \rvert}{\lvert f'(z_n) \rvert } < \varepsilon$$

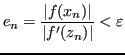
ovvero, intuitivamente, l'arresto avviene quando il residuo è abbastanza piccolo e la pendenza abbastanza grande.

L'approccio nella pratica dipende se si abbiano informazioni su $f'$ (si potrebbero non avere affatto informazioni sulla funzione, vista come una black box).