Next: Arresto per stima a Up: Criteri di Arresto Previous: Criteri di Arresto Indice Indice analitico
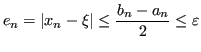
Preso un intervallo iniziale ![]() =
= ![]() ,
,
![]() , anche se la situazione migliorerà con
, anche se la situazione migliorerà con ![]() abbastanza grande:
abbastanza grande:
| n | |||
| 0 | 1 | 5 | 3 |
| 1 | 1 | 3 | 2 |
| ... | ... | ... | ... |
![]()
Matteo Lisotto, Tobia Tesan - CC-BY 2.0