Velocità di Convergenza

Le successioni $a_n$, $b_n$, $x_n$ godono delle seguenti proprietà:

Teorema 3.4  

$$b_n - a_n = \frac{b-a}{2^n}$$

Teorema 3.5  

$$\lvert a_n - \xi \rvert, \lvert b_n - \xi \rvert \le \max({\lvert a_n - \xi \rvert, \lvert b_n - \xi \rvert}) < b_n - a_n = \frac{b-a}{2^n}$$

Teorema 3.6  

$$0 < e_n = \lvert x_n - \xi \rvert < \frac{b_n-a_n}{2} = \frac{b-a}{2^{n+1}}$$

Teorema 3.7  

$$\lim_{n \to \infty} a_n = \lim_{n \to \infty} b_n =\lim_{n \to \infty} x_n = \xi$$

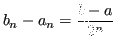
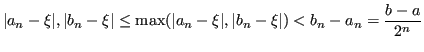
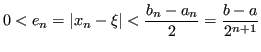
La convergenza del metodo di bisezione è molto lenta.

È difficile trarre conclusioni generali oltre ad affermare che l'errore $e_n$ è maggiorato da una successione $s_n$ tale che $s_{n+1} = \frac{1}{2} s_n$.

Lemma 3.2 (Velocità di guadagno delle cifre significative)   La velocità di convergenza del metodo di bisezione è logaritmica.

Per guadagnare una cifra significativa nell'approssimazione di $\xi$, ossia per avere

$$\vert x_n - \xi\vert = \frac{\vert x_m - \xi\vert}{10}$$

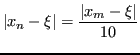
Occorrono $n - m = log_2 (10) \approx 3.32$ iterazioni.