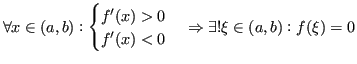Esistenza di soluzioni
Teorema 3.2
Esiste certamente una soluzione a cui il metodo di bisezione converge se la funzione soddisfa le condizioni del teorema degli zeri:
Inoltre:
Teorema 3.3
La soluzione è anche unica se la funzione è strettamente crescente o decrescente nell'intervallo 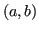 :
:
Matteo Lisotto, Tobia Tesan - CC-BY 2.0