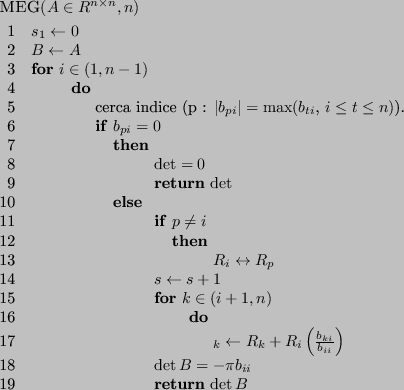Next: Soluzione numerica di equazioni Up: Fondamenti del Calcolo Numerico Previous: Condizionamento di una funzione Indice Indice analitico
Il costo computazionale espresso in operazioni piuttosto che in tempo di esecuzione e' una buona misura perchè è slegato dalla potenza del calcolatore di destinazione, ma non tiene conto del flusso delle istruzioni.
Algoritmi diversi per risolvere lo stesso problema hanno potenzialmente complessità diverse.
Sia ![]() un polinomio qualsiasi
un polinomio qualsiasi
L'algoritmo di Hörner consiste nel rappresentare il polinomio come:
Si vuole calcolare una potenza ![]() , dove
, dove
![]() .
.
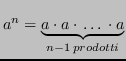
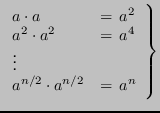
In caso contrario, si può considerare la rappresentazione in base 2 dell'esponente:
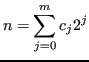 |
|
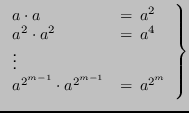
L'algoritmo impiega ![]() operazioni per calcolare i singoli fattori
operazioni per calcolare i singoli fattori
![]() , e un certo numero di prodotti tra essi per ottenere
, e un certo numero di prodotti tra essi per ottenere ![]() , al più
, al più ![]() (se
(se ![]() , si risparmia un prodotto).
, si risparmia un prodotto).
La complessità ![]() è quindi al più
è quindi al più ![]() .
.
Data la seguente matrice
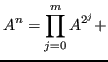 eventuali m prodotti di matrici
eventuali m prodotti di matrici
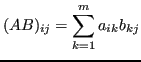
Consideriamo il problema di calcolare ![]() .
Sia
.
Sia ![]() , allora è noto che
, allora è noto che
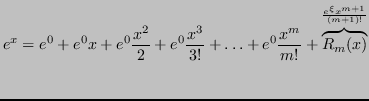
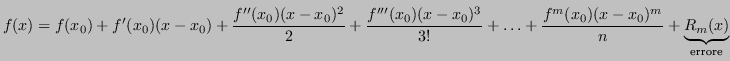
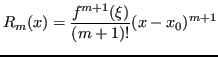 con
con
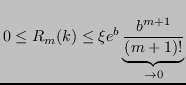
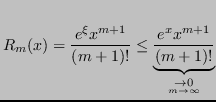
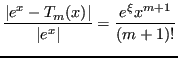
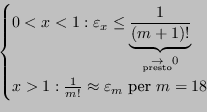
Consideriamo il problema di calcolare il determinante di una matrice
![]() .
.
La sviluppo di Laplace è un metodo particolarmente inefficiente di calcolare il determinante3:
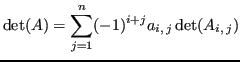
dove ![]() è una matrice
è una matrice
![]() ottenuta da
ottenuta da ![]() cancellando la riga
cancellando la riga ![]() -esima e la colonna
-esima e la colonna ![]() -esima.
-esima.
Il costo del calcolo del determinante di ![]() con Laplace è
con Laplace è
![]() e il numero di moltiplicazioni necessario è
e il numero di moltiplicazioni necessario è
![]() .
.
| n | t @ 1GFLOPS | t @ 1TFLOPS |
| 10 | 4 ms | - |
| 15 | 24 minuti | - |
| 20 | 154 anni | |
| 25 | ||
| 100 |
Dove
![]() è una sequenza di mosse di Gauss risulta in una matrice triangolare superiore
è una sequenza di mosse di Gauss risulta in una matrice triangolare superiore ![]() tale che
tale che
![]()
Ricordiamo le proprietà del determinante:
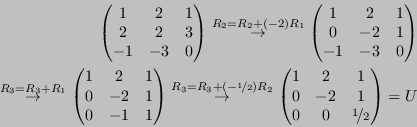
L'algoritmo del MEG è un algoritmo finito, ma delicato da trattare in aritmetica di macchina.