Next: Complessità computazionale Up: Condizionamento Previous: Calcolo di Indice Indice analitico
Quello che ci si troverà a risolvere in macchina è in reltà un problema:
![]() è una funzione perturbata (a causa di operazioni eseguite in aritmetica finita, con possibili errori di di discretizzazione e/o convergenza) su un dato a sua volta perturbato (a causa dell'errore di rappresentazione sempre presente o dell'origine sperimentale del dato).
è una funzione perturbata (a causa di operazioni eseguite in aritmetica finita, con possibili errori di di discretizzazione e/o convergenza) su un dato a sua volta perturbato (a causa dell'errore di rappresentazione sempre presente o dell'origine sperimentale del dato).
Per semplicità si studierà il problema
![]() , considerando il metodo numerico come eseguito in artimetica esatta.
, considerando il metodo numerico come eseguito in artimetica esatta.
Contrariamente, un problema mal condizionato è un problema in cui la soluzione è molto sensibile a piccole perturbazioni nei dati.
Dove
![]() è l'errore relativo sull'input,
è l'errore relativo sull'input,
![]() è l'errore relativo sul risultato.
è l'errore relativo sul risultato.
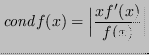
E quindi nelle vicinanze di ![]() :
:
Allora
Applicando la consueta definizione di errore relativo
![]() :
:
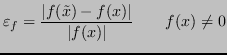
È possibile riscrivere:
![]()
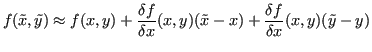
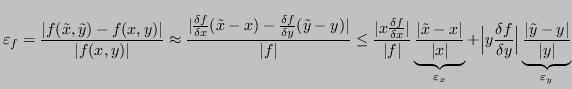
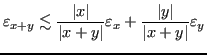
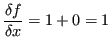
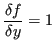
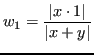
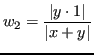
Come visto in precedenza, la somma algebrica è una funzione ben condizionata se non è vero che
![]() .
.
Calcolando ![]() in
in
![]() :
:
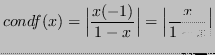
![]() è una funzione mal condizionata (per
è una funzione mal condizionata (per
![]() )
)
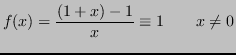
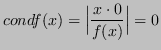
In questo caso, ad esempio la funzione è in una forma notoriamente instabile per
![]() .
.
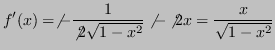
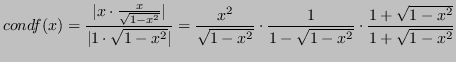
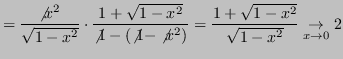
Questa ![]() è ben condizionata, ma l'algoritmo è instabile.
E' possibile correggerlo cosi':
è ben condizionata, ma l'algoritmo è instabile.
E' possibile correggerlo cosi':
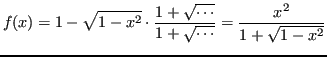
L'algoritmo è allora stabile (per
![]() ).
).
Matteo Lisotto, Tobia Tesan - CC-BY 2.0