Calcolo di $\pi$

Esempio 2.7 (Formula di Viète o Archimede per il calcolo di $\pi$)  

Si consideri la seguente successione, dovuta a François Viète e basata sul metodo di Archimede per il calcolo di $\pi$:

$$\begin{cases}z_2 = 2 \\ z_{n+1} = 2^{n-\frac{1}{2}} \sqrt{1-\sqrt{1-4^{1-n}z_n^2}} \end{cases}$$

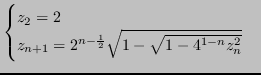
Vale:

$$\lim_{n \to \infty} z_n = \pi$$

Il calcolo della successione è caratterizzato da un errore che oltre una certa soglia cresce, a causa dell'influenza crescente delle sottrazioni necessarie.

Poichè $\alpha_n \to 0$ per $n \to +\infty$, si ottiene una sottrazione tra due termini $x$ e $y$ che si avvicinano sempre di più.

L'errore che ne deriva cresce esponenzialmente con $n$:

$$\omega_2(x,\,y) = \frac{\vert y\vert}{\vert x+y\vert} = \frac{\sqrt{1-\alpha_n}}{1-\sqrt{1-\alpha_n}} =$$

$$= \frac{1 + \sqrt{1-\alpha_n}}{1+\sqrt{1-\alpha_n}} \,\, \frac{\s... ...+\sqrt{1-\alpha_n})}{1-(1-\alpha_n)} = \frac{2}{\alpha_n} = \frac{4^n}{2 z_n^2}$$

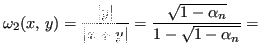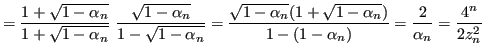È necessario rendere stabile la sottrazione $1 - \sqrt{1-\alpha_n}$:

$$1-\sqrt{1-\alpha_n} \,\, \frac{1+\sqrt{1-\alpha_n}}{1+\sqrt{1-\al... ...ac{1-(1-\alpha_n)}{1+\sqrt{1-\alpha_n}} = \frac{\alpha_n}{1+\sqrt{1-\alpha_n}}$$

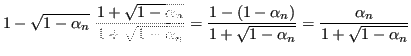
Sostituendo, si ottiene una nuova successione algebricamente equivalente, ma scritta in modo stabile.

$$\left\{ \begin{array}{ll} z_2 = 2 \\ z_{n+1} = \frac{\sqrt{2}(z_n)}{\sqrt{1+\sqrt{1-\alpha_n}}} \end{array} \right.$$

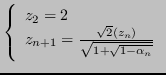
Una successione alternativa deriva dalla serie geometrica:

$$\sum_{j = 1}^{+\infty} \frac{1}{j^2}$$

Essa converge a $\frac{\pi^2}{6}$, e la sua successione di somme parziali è esprimibile come:

$$\left\{ \begin{array}{ll} S_1 = 1 \\ S_{n+1} = S_n + \frac{1}{(n+1)^2} \end{array} \right. \quad n = 1,\,2,\,\dots$$

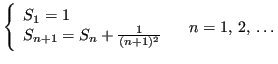
Da essa si può costruire una seconda successione $\{u_n\}$ con $u_n = \sqrt{6 S_n}$, convergente a $\pi$:

$$\lim_{n \to +\infty} u_n = \pi$$

L'algoritmo è stabile, ma non è utilizzato poichè converge molto lentamente.

In particolare, l'errore commesso rispetto a $\pi$ decade con un fattore $\frac{1}{n}$: per ottenere, ad esempio, una precisione di $10^{-16}$, sono necessarie $10^{16}$ iterazioni.