Next: Calcolo di Up: Condizionamento Previous: Condizionamento delle operazioni elementari Indice Indice analitico
La soluzione delle equazioni di secondo grado è un problema ben condizionato, ma l'usuale formula può portare a perdita di precisione.
Si consideri l'equazione di secondo grado:
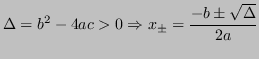
Esistono due possibili casi:
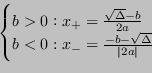
Nel primo caso al numeratore si presenta una sottrazione.
Se dovessero essere ![]() ,
, ![]() ,
, ![]() tali che
tali che
![]() allora (in termini relativi):
allora (in termini relativi):
Allora
![]() e a causa delle proprietà della sottrazione in macchina
e a causa delle proprietà della sottrazione in macchina ![]() si avrebbe perdita di precisione nel calcolo di
si avrebbe perdita di precisione nel calcolo di
![]() :
:
È però sufficiente manipolare algebricamente l'![]() problematico per rimuovere l'operazione instabile:
problematico per rimuovere l'operazione instabile:
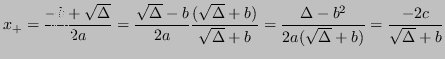
Dunque
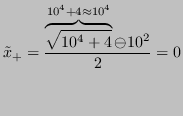
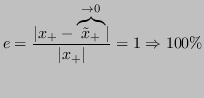
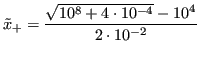
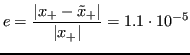
Matteo Lisotto, Tobia Tesan - CC-BY 2.0