Next: Condizionamento del calcolo soluzioni Up: Condizionamento Previous: Condizionamento Indice Indice analitico
Interessa sapere in che modo un errore su (la rappresentazione approssimata de) i dati iniziali del problema può influenzare il risultato finale.
Si vuole ossia ossia studiare il condizionamento di un'operazione - se piccoli errori nei dati in ingresso causino piccoli o grandi errori nel risultato e se le operazioni siano dunque stabili o meno.
Siano
![]() e
e
![]() , si definisce allora:
, si definisce allora:
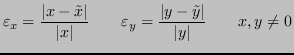
Poichè
![]() segue per definizione di
segue per definizione di
![]() che
che
![]() .
.
Si vuole trovare, per ciascuna operazione, un limite superiore per
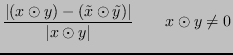
L'errore necessariamente introdotto dalla rappresentazione del risultato è trascurabile:
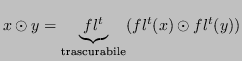
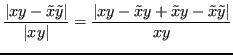
È possibile applicare la disuguaglianza triangolare (
![]() ) su
) su
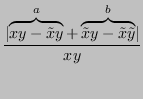
e scrivere
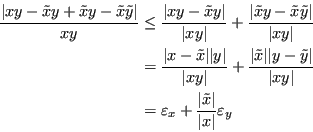
E poichè
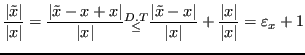
Si può scrivere
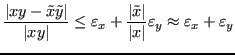
L'errore sul prodotto resta dunque dello stesso ordine di grandezza degli errori sui dati.
![]()
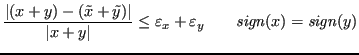
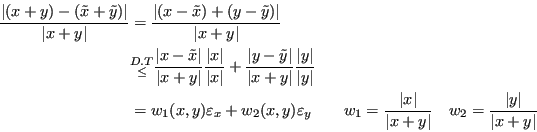
In caso di addendi di segno discorde:
![]() .
In particolare, se
.
In particolare, se
![]() allora
allora
![]() .
.
Poichè:
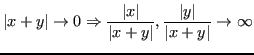
Allora:
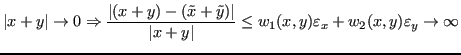
![]()
Matteo Lisotto, Tobia Tesan - CC-BY 2.0