Next: Metodo delle secanti Up: Altri metodi Previous: Altri metodi Indice Indice analitico
Il metodo consiste nel costruire una successione di punti dove, assegnato un punto iniziale ![]()
![]() il punto
il punto ![]() sia lo zero della retta passante per il punto iniziale
sia lo zero della retta passante per il punto iniziale
![]() e di coefficiente angolare:
e di coefficiente angolare:
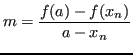
Matteo Lisotto, Tobia Tesan - CC-BY 2.0