Next: Condizionamento Up: Operazioni con numeri macchina Previous: Operazioni con numeri macchina Indice Indice analitico
Lavorando su numeri interi, se il risultato dell'operazione cade all'interno dell'insieme di rappresentabilità, le operazioni coincidono con quelle algebriche.
Considerando invece i numeri reali, le operazioni saranno definite solo su numeri di macchina e dovranno avere per risultato ancora un numero di macchina; ovvero ad esempio nel caso dell'addizione si ha che
![]() .
.
In particolare:
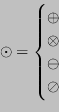
Si userà la seguente notazione per indicare un'operazione macchina:
Per rappresentare il risultato servirebbero 17 cifre di mantissa, ma ![]() .
.
Allora, in macchina:
Poichè l'ultima cifra viene arrotondata a 0.
![]() si comporta dunque da elemento neutro, in aggiunta a 0.
si comporta dunque da elemento neutro, in aggiunta a 0.
![]()
![]() è ossia il più piccolo numero macchina che non si comporta come elemento neutro.
è ossia il più piccolo numero macchina che non si comporta come elemento neutro.
E' evidente che
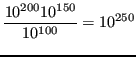
Ma sebbene, correttamente,
Eliminando le parentesi e dunque alterando l'ordine in cui vengono effettuate le operazioni, il risultato viene inficiato da un overflow che prima non si manifestava:
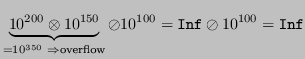
![]()
Matteo Lisotto, Tobia Tesan - CC-BY 2.0